Non-Arbitrage Conditions for Perpetual Forwards
This paper explores how a perpetual future’s mark price should respond to known future changes in oracle price. This will be a common scenario as equity perpetual oracles handle rolling contracts, with pronounced effects for high dividend paying stocks. The solution is to found stepping backwards using non-arbitrage conditions. We show that under such conditions, trade.xyz’s design captures the dividend in the form of funding payments to longs.
Introduction
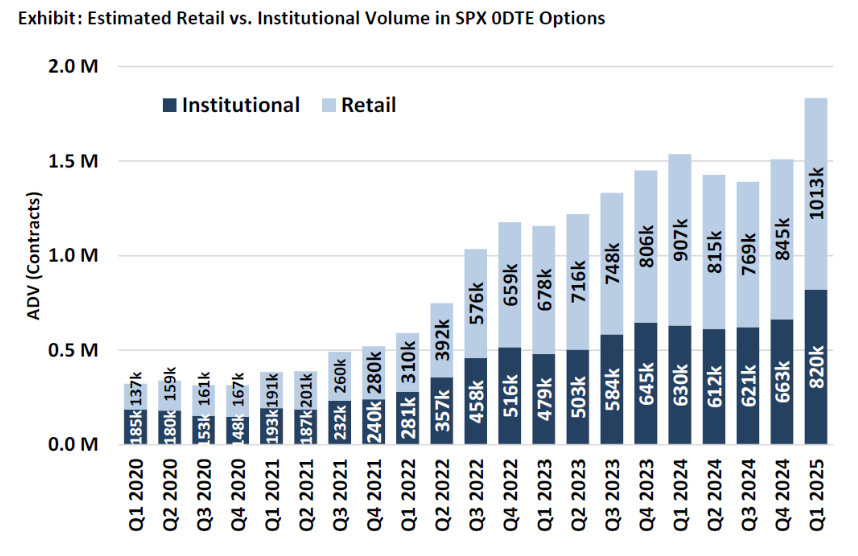
Equity perpetual futures are the inevitable collision of crypto’s greatest invention and the largest speculation market in the world. In the author’s opinion, perps are the correct instrument to express delta leverage positions, especially non-event based. This describes the majority of retail speculation, as seen by 0DTE option volume growth (the highest cheapest delta leverage possible).
This intersection of old and new finance brings new design choices. The topic here is: how do you price known future events like dividends into an instrument that never expires (perpetuals).
Why Aren’t Dividends Free Money For Puts?
TardFi contracts like futures and options have expiration dates, which means they have a forward price. A forward price takes into account all available information—especially interest rates and dividends—to calculate the price at expiration given the current spot.
the simplified forward prices for non-dividend and dividend stocks with interest rate r and dividend yield d:
A put option already prices in any relevant dividends through the forward, so there is no free money to be made. This is called a non-arbitrage condition.
A forward (with expiration < T0) vs spot price for a $100 stock with a $2 dividend on T0
Perpetuals obviously never expire, which makes pricing future events interesting. This hasn’t been a problem with Bitcoin, as Bitcoin has no dividends. But as the first liquid equity perpetual NASDAQ contracts go live on trade.xyz, now is a good time to think about it.
How Do Perps Work?
A quick primer on how perpetual futures work, since it will be needed later. Feel free to skip.
Perpetual futures are synthetic contracts that track an underlying ”oracle price” through a funding mechanism. If the perpetual’s mark price is above the oracle, the funding is positive, and longs pay shorts a small % of their notional every period. This incentivizes selling through closing longs or opening shorts, which pushes the mark price down towards the oracle.
Vice versa, if the perps mark is below the oracle, the funding is negative, and shorts pay, which incentivizes buying through shorts closing or new longs opening.
This filter ensures that on long enough timeframes the perpetual tracks the oracle, although in times of volatility this relationship can break down due to stronger external forces (liquidations).
Note there is always a 1:1 ratio of longs to shorts (when a long is opened either a short is opened or a long is closed).
What Oracles Do Crypto Perps Use?
For most crypto perpetual exchanges, the oracle of an asset is simply an index of spot prices. This allows the cost of capital (both interest rates and ”borrow”) to get abstracted into a relatively continuously settled funding rate.
This works well. For example, in times of froth, when people want extra money to go long, the mark to oracle premium drifts up to an agreeable funding rate.
https://hyperliquid.gitbook.io/hyperliquid- docs/trading/funding
What Oracles Do Equity Perps Use?
While we don’t have many examples yet, trade.xyz’s perpetual model can be explored here, as it’s rational. trade.xyz backs out a spot price from the forward price of the front quarterly future.
https://docs.trade.xyz/xyz-perps-specification/equity- perpetuals/xyz100-and-index-perpetuals
This forward price only captures dividend events before expiration T. As the oracle rolls over to the next quarterly, it will price in the next set of dividends and go down accordingly. This presents a funding/forward arbitrage if not properly priced. While the NASDAQ has a measly ∼0.46% annual dividend yield, for higher dividend paying stocks it is a potential opportunity. Markets are only efficient because people make them efficient.
What Is The Arbitrage?
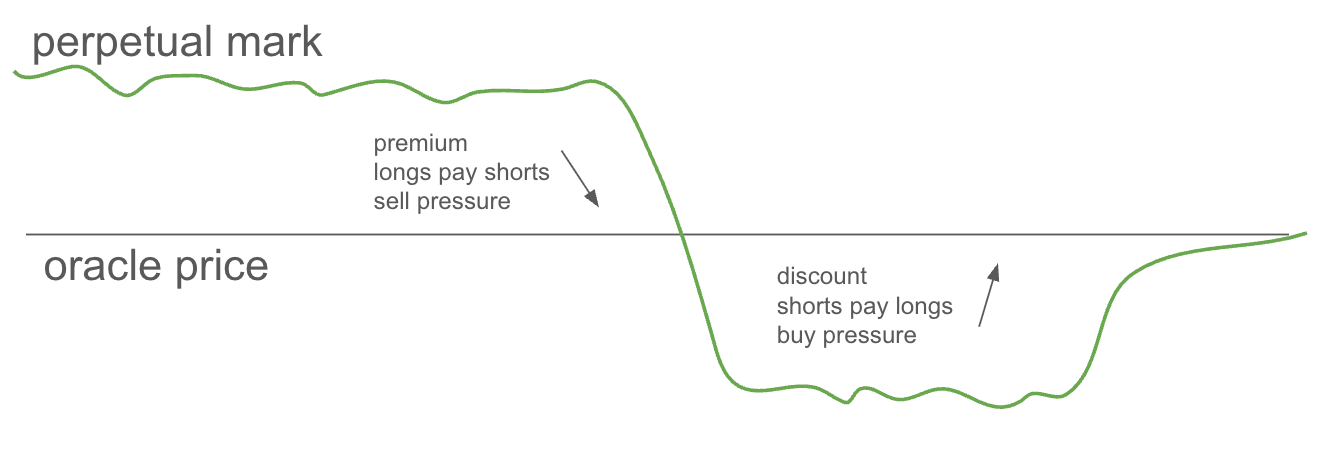
In isolation, if no one else does anything, one could short the perpetual with very little time left in the last funding period before the oracle roll, while simultaneously buying the next quarter’s future. This would give you no delta exposure to the underlying, while benefiting from the perp’s oracle basis collapsing.
In practice, the mark will discount below the oracle leading into the contract roll.
Here we will explore how to think about this discount curve backwards from non-arbitrage condition principles.
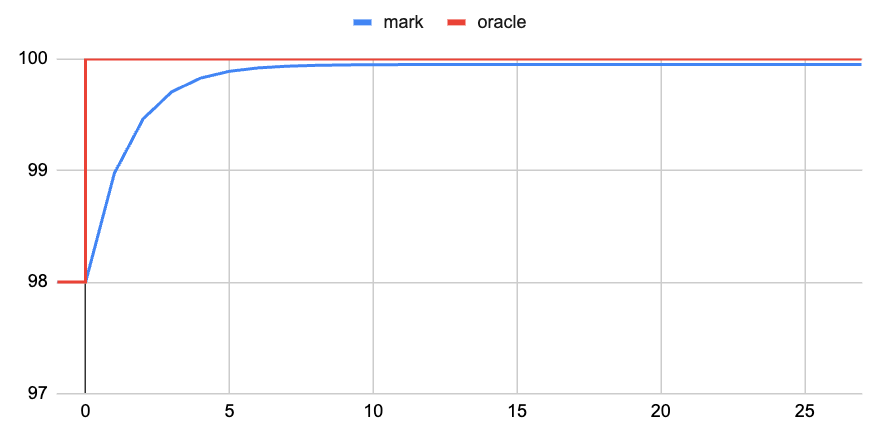
Let’s take a fictional $100 stock paying a $2 dividend at some date in the future. On date/time T the perpetual’s oracle will roll to a contract that includes this dividend. We will assume no cost of capital.
Given the oracle price will go down $2 to $98 on T , the mark price must discount from oracle into T such that shorts pay longs $2. The way to think about this is to solve backwards, from T to T − 1 funding period.
For T − 1, the further drop from mark to $98 must equal the funding rates shorts pay for T − 1, or one could arbitrage the difference, by either longing or shorting the perp and hedging with the future. The funding rate shorts pay longs also depends on the difference between oracle and mark, so you can solve for mark.
where x is the non-arbitrage mark price for T-1, o is the oracle price, and d is:
For our fictional $100 oracle going to $98 at T, for Hyperliquid’s one hour funding model, x works out to $98.975. At $98.975, shorts will pay $0.975 in funding to longs, while benefitting from a final $0.975 price drop as the oracle rolls to $98.
You then repeat this process for T − 2, replacing the old $98 destination price with $98.975 (so d = −1.025% instead of -2%). This results in a non-arbitrage price of $99.4625. This process is repeated until you approach the neutral funding rate, at which point capital costs drown out any effects of the oracle roll.
Non-Arbitrage Conditions
This process can be repeated to construct the non- arbitrage condition discount curve for the mark price rel- ative to an oracle price.
Any upwards deviation from this discount curve would mean you could short the perp and buy the future and pay less in funding than the perp basis collapse. Any downwards means you could buy the perp and sell the future and receive more in funding than the basis collapse.
Under these conditions, the long side of equity perps for trade.xyz’s design elegantly receives the dividend payment in the form of funding, equivalent to holding the underlying spot.
Piecewise Solution
Simplifying the equation, the min max clamp results in some weird piecewise math, reducing from:
to
now define y as:
then:
next we express the clamp only in terms of y
so we just need to solve:
solving piecewise by region of the clamp:
region 1: y < -0.0004
then c = 0.0005
check boundaries:
valid when d < -0.0003.
region 2: −0.0004 ≤ y ≤ 0.0006
then c = 0.0001 − y
check boundaries:
valid when −0.0003 ≤ d ≤ 0.0007.
region 3: y > 0.0006
then c = −0.0005
check boundaries:
valid when d > 0.0007.
so the final piecewise solution is:
and then:
where x is the non-arbitrage mark price for the funding period given a known discount d, for hourly funding rate according to Hyperliquid and trade.xyz’s funding rate and clamp, with o = oracle.
Further Problems To Explore
One critical problem for perpetual exchanges to solve is: how to handle known future gap volatility (earnings)? If the option market is pricing a ∼20% implied move for earnings, someone going 10x long and 10x short will lose 100% on the wrong side but make 200% on the right side—an arbitrage condition. Isolating the market and ADL-ing profits is a bad experience for the correct side. ADL-ing before is a bad experience for everyone. Things to think about.